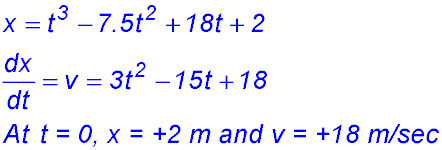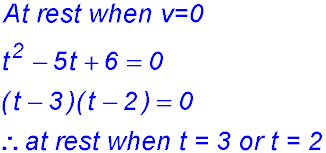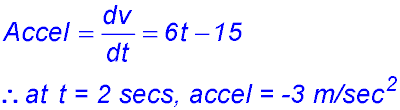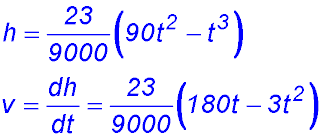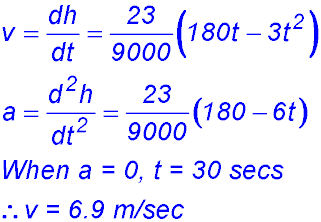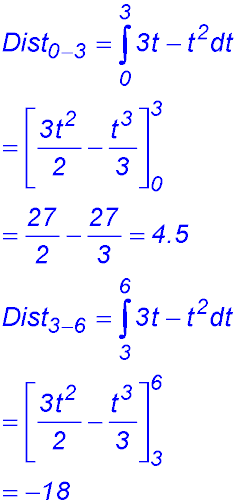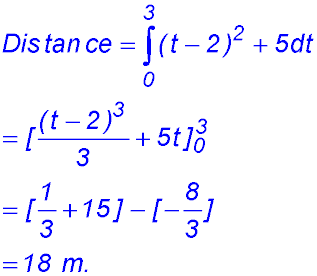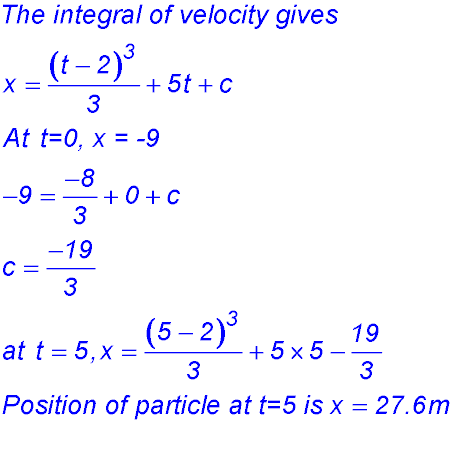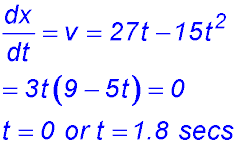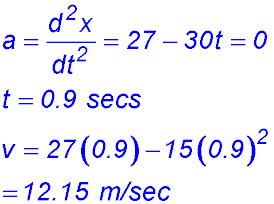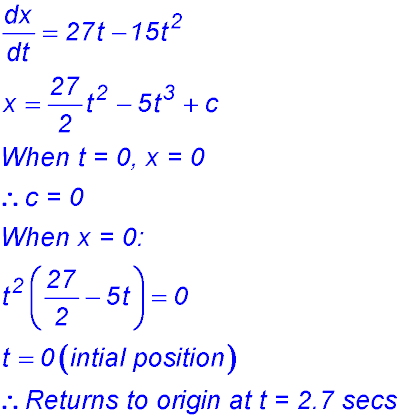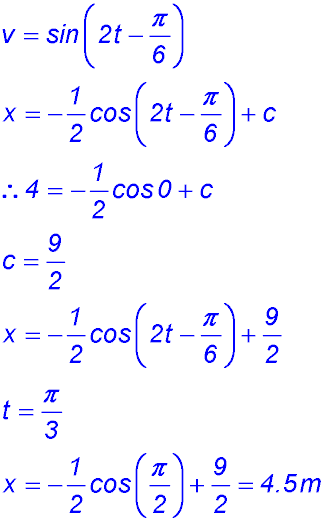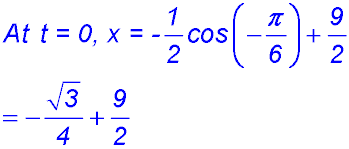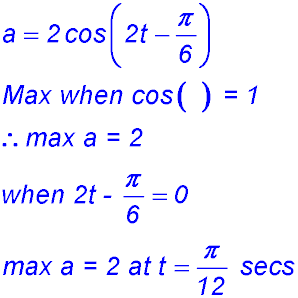Where the techniques of Maths
are explained in simple terms.
Applications of Calculus - Equations of motion in one direction.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Given displacement equation | 1. s(t) = t3 - 12t2 + 36t
(i) Find an expression for the velocity v(t) and acceleration a(t) of the particle in terms of t.
(ii) When is the particle at rest?
(iii) When does the particle reach its maximum velocity in the negative direction?
(iv) Complete the table:.
|
||||||||||||||||||||||||
| 2. x(t) = 3t2 - t3 for t ≥ 0.
(i) Find the initial velocity and acceleration particle.
(iii) Determine the time at which the acceleration of the particle is zero.
(iv) Graph the function x(t), t ≥ 0. (v) Determine the total distance travelled by the particle in the first 4 seconds.
(vi) Describe the motion of the particle.
|
|||||||||||||||||||||||||
3. (i) Find the particle's initial position and velocity.
|
|||||||||||||||||||||||||
| 4. x = t(t - 6)2 = t3 - 12t2 + 36t
(easier to expand now). (i) Find the initial position of the body. t = 0, x = 0 so at the origin. (ii) When is the body again at this position? When x = 0, t = 0 or 6. So at the origin again at x = 6 seconds. (iii) Obtain the velocity and accelerations functions for the motion. Velocity = 3t2 - 24t + 36 Accel = 6t - 24 (iv) At what times is the body momentarily at rest? When velocity = 0 Velocity = 3(t2 - 8t+12) = 3(t - 2)(t - 6) ∴ at rest at t = 2 and t = 6 seconds. (v) In which direction does the body move between these times? Try t = 3, v = -9 so body moves in a negative direction (i.e. towards the left). Rather than try t = 3, we could have said for values between 2 and 6, velocity is negative by looking at the factored equation. (vi) What is the initial acceleration for the motion? Is it tending to slow down or speed up the initial movement? t = 0, acceleration = -24 m/sec2. The negative acceleration is slowing down the motion which started at 36 m/sec. Hence it stops at 2 secs. (vii) At what instant is there no acceleration acting on the moving body? What is the velocity at that instant? Show that this is the greatest speed in a negative direction attained by the moving body. When accel = 0, 6t - 24 = 0 so t = 4 secs. At t = 4, velocity = -12 m/sec. The form of the velocity equation is a concave up parabola with zeros at t = 2 and t = 6. Hence the maximum speed in the negative direction is reached half way between those times. (viii) Draw graphs to show each of the displacement, velocity and acceleration functions.
|
|||||||||||||||||||||||||
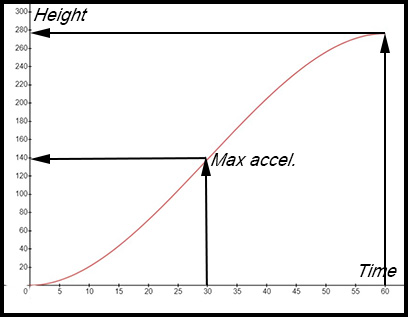
5. 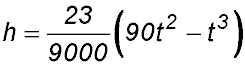 . .
(i)
(ii) When at rest, v = 0 ∴ 3t(60 - t) = 0 t = 60 secs (iii) When t = 60, h = 276 m. (iv) When the lift is travelling fastest, acceleration = 0.
(v) |
|||||||||||||||||||||||||
| Log function | 6. | ||||||||||||||||||||||||
| 7. | |||||||||||||||||||||||||
| 8. | |||||||||||||||||||||||||
| Exponential function | 9. | ||||||||||||||||||||||||
| 10. (i) What is the initial velocity of the particle?
When t = 0, v = 2(2 - 0)e0 = 4 m/sec. (ii) When and where will the particle be at rest? When v = 0, t = 2 secs (as the exponential component can't = 0). (iii) Find the time when the particle has zero acceleration.
(iv) What is the time interval when the particle is increasing its speed? Speed increases either when vel > 0 and accel > 0 OR when vel < 0 and accel < 0. Here speed > 0 up to t = 2 and then it becomes -ve. Accel is -ve up to t = 4. Up to 2 seconds, speed > 0 and accel < 0 - so no increase. The only interval is therefore 2 < t < 4 because here both speed < 0 and a < 0. Difficult. |
|||||||||||||||||||||||||
| 11 | |||||||||||||||||||||||||
| Trig function | 12. A particle is moving along the x-axis. Its position at time t is given by x = t + sin t.
(i) At what times during the period 0 < t < 3π is the particle stationary?
(ii) At what times during the period 0 < t < 3π is the acceleration equal to zero?
(iii) Sketch the graph x = t + sin t for 0 < t < 3π. Clearly label any stationary points and any points of inflexion. |
||||||||||||||||||||||||
| 13. | |||||||||||||||||||||||||
| 14. | |||||||||||||||||||||||||
| Given velocity equation | 17. (i) (ii) & (iii) (iv) Displacement = 18 m to the left. |
||||||||||||||||||||||||
18. The velocity v m/sec of an object at time t seconds is given by v = 3t2 - 14t + 8. The object is initially 30 m to the right of the origin.
|
|||||||||||||||||||||||||
| 19. (i) Find the minimum speed of the particle.
The equation for velocity is v = (t - 2)2 + 5. The first term must be positive (it is a square) then 5 is added. When the first term is 0 at t = 2, minimum velocity must be 5 m/sec. (ii) Find the initial acceleration of the particle. a = 2(t - 2) so when t = 0, acceleration is -4 m/sec2. (iii) Find the distance travelled by the particle in the first 3 seconds. The velocity is always positive, so there is no problem about calculating distance in two parts. Just integrate because the area under the velocity curve is the distance travelled.
(iv) Initially the particle is at 9 m to the left of the origin. Find the position of the particle at t = 5 secs.
|
|||||||||||||||||||||||||
20. (i) (ii) (iii) |
|||||||||||||||||||||||||
21. (i) (ii) Distance travelled must be split into two parts: Distance from t = 0 to t = π/12 and then to t = π/3:
(iii) |
|||||||||||||||||||||||||
| Given acceleration equation. | 22. | ||||||||||||||||||||||||
| 23. | |||||||||||||||||||||||||